title: "DSA Assignment 1"
date: 2023-09-16
author: AllenYGY
status: DONE
created: 2024-01-16T21:03
updated: 2024-06-11T01:14
publish: TrueDSA Assignment 1
Problem I
Algorithm GETminimum(A)
SORT(A)
if A[0]−A[A.length−1]<0 then
return A[0]−A[A.length−1]
else
min←∞
for i←1 to A.length−1 do
if A[i]−A[i−1]<min then
min←A[i]−A[i−1]
end if
end for
end if
return min
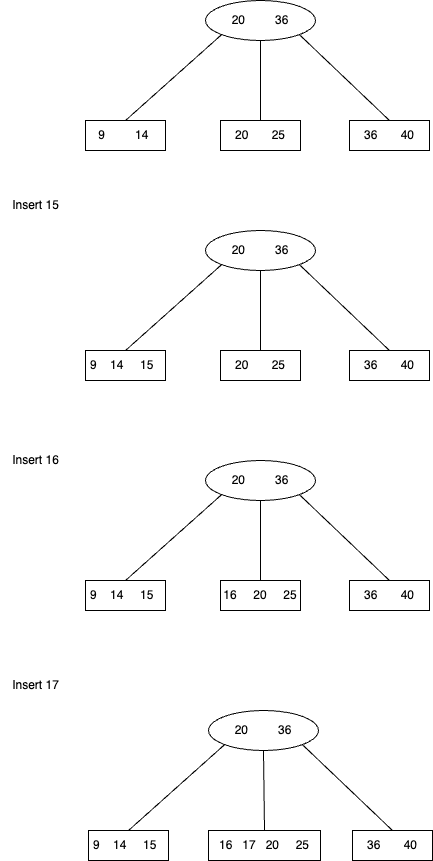
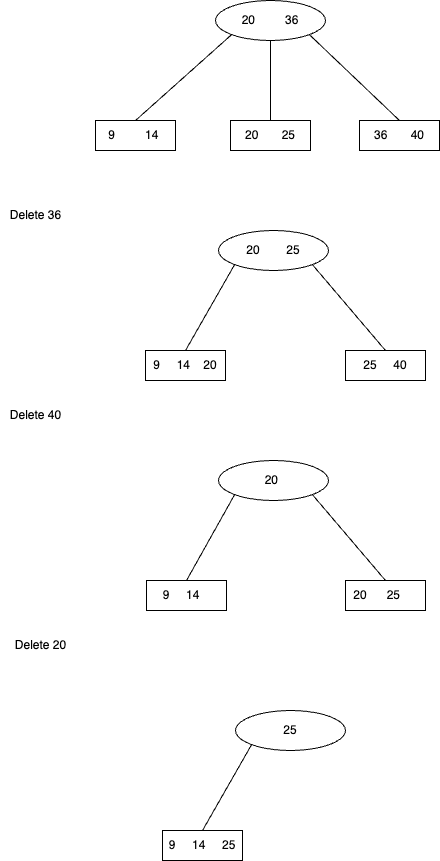
Problem II
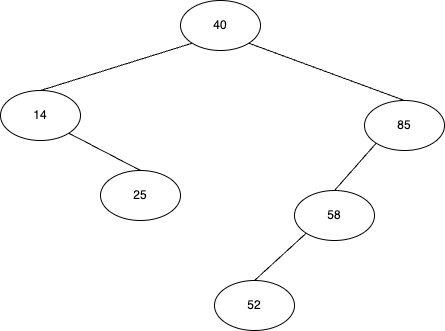
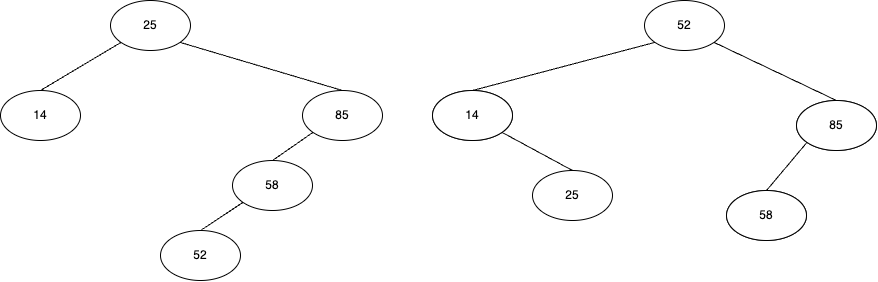
- |14|25|40|52|58|85|
Problem III
3.1
a.
Initial State
52|2
┌───────┴───────┐
15|1 85|0
┌───┴───┐
8|0 31|0
Insert 82:
52|2
┌───────┴───────┐
15|1 85|1
┌───┴───┐ ┌───┘
8|0 31|0 82|0
Insert 6:
52|3
┌───────────────┴───────────────┐
15|2 85|1
┌───────┴───────┐ ┌───────┘
8|1 31|0 82|0
┌───┘
6|0
Insert 65:
52|3
┌───────────────┴───────────────┐
15|2 82|1
┌───────┴───────┐ ┌───────┴───────┐
8|1 31|0 65|0 85|0
┌───┘
6|0
b.
1
52|3
┌───────────────┴───────────────┐
8|1 82|2
┌───────┴───────┐ ┌───────┴───────┐
6|0 15|0 65|1 85|1
└───┐ └───┐
72|0 95|0
2
65|3
┌───────────────┴───────────────┐
15|2 82|2
┌───────┴───────┐ ┌───────┴───────┐
8|1 31|0 72|0 85|1
┌───┘ └───┐
6|0 95|0
3
52|3
┌───────────────┴───────────────┐
15|2 85|2
┌───────┴───────┐ ┌───────┴───────┐
8|1 31|0 65|1 95|0
┌───┘ └───┐
6|0 72|0
3.2
-
Insertion Time: To insert an element into an AVLAVL tree, we perform a binary search to find the correct position for the new element and then possibly perform some rotations to maintain the AVLAVL property. The time complexity of both these operations is
-
Building the Tree: If we insert
-
In-order Traversal: Once the AVLAVL tree is built, we can perform an in-order traversal to retrieve the elements in sorted order. An in-order traversal of a binary search tree visits the nodes in ascending order, which is what we want for sorting. The time complexity for in-order traversal is
-
Total Time Complexity: The total time complexity of sorting an array using an AVLAVL tree is the time to build the tree (
Therefore, we have shown that using an |AVL tree to sort an array of distinct integers has a time complexity of
Problem IV
a.
b.