date: 2024-10-25
title: BDA-Review
status: DONE
author:
  - AllenYGY
tags:
  - Review
  - BDA
  - Project
publish: true

BDA-Review

1. Motivation

In the decision-making process of movie investments, predicting box office performance is a critical step. By analyzing key factors, investors can reasonably evaluate a movie’s box office potential before production, which helps guide production and marketing strategies. This not only increases the movie's box office potential but also enables investors to make optimal decisions given limited resources (such as selecting the right actors, determining the marketing budget, etc.).

2. What is Causal Inference?

Causal inference is the process of identifying and understanding the cause-and-effect relationships between variables.

2.1 Correlation does not imply causation:

Two variables might show a high degree of correlation, but that does not mean there is a causal relationship between them.
For example, there may be a high correlation between increased ice cream sales and drowning incidents during the summer, but ice cream sales are not the cause of drowning. This type of error often occurs in traditional correlation-based analyses.

2.2 Simpson's Paradox:

Simpson's paradox is a phenomenon in probability and statistics in which a trend appears in several groups of data but disappears or reverses when the groups are combined.
For example, in the figure below, the graph illustrates the relationship between Cholesterol levels (y-axis) and Exercise (x-axis).

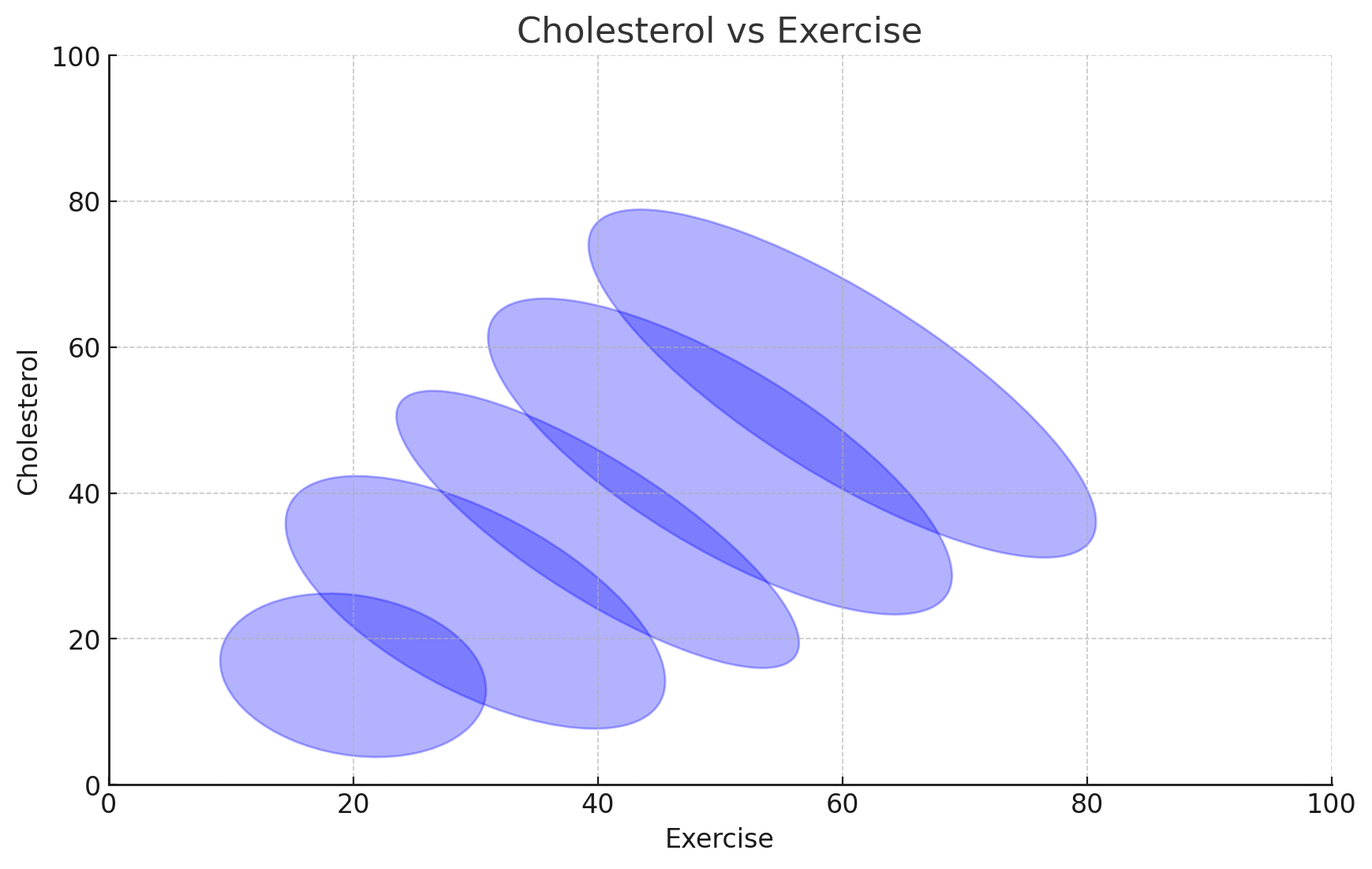
Intuitively, Exercise and Cholesterol levels are positively correlated.

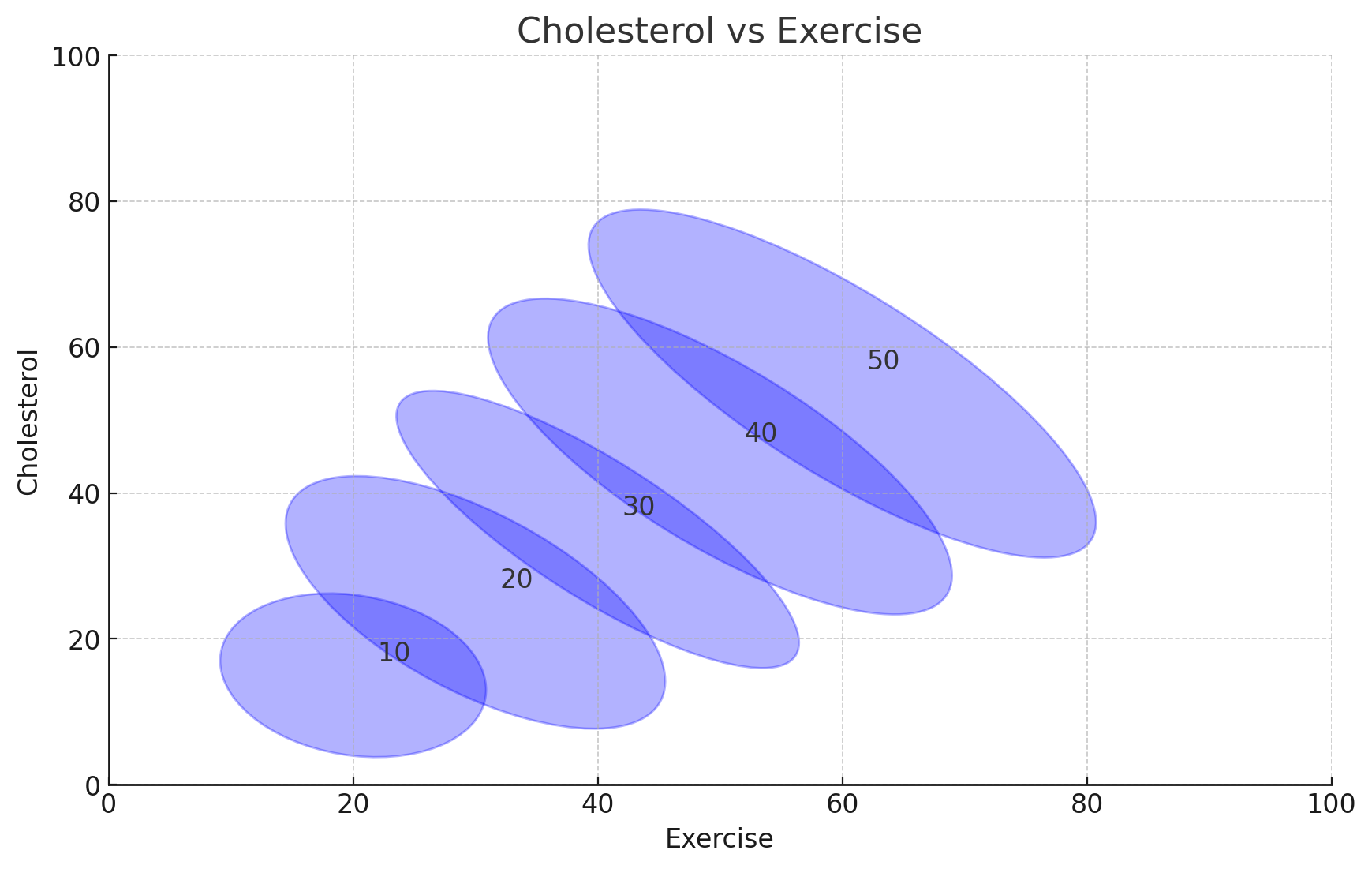
Each eclipse is a group of age, for each age group, Exercise and Cholesterol are negatively correlated.

3. Why Use Causal Inference?

3.1. Causal Inference and Causal Graphical Models

In traditional box office prediction methods, researchers often use correlation analysis to identify relationships between various variables (e.g., actors, directors, movie genres) and box office outcomes. However, correlation does not imply causation; even if two variables show strong correlation, it does not necessarily mean that one variable causes the other to change. For instance, there might be a high correlation between a movie's marketing budget and box office performance, but an increase in the marketing budget might not be the direct cause of increased box office revenue, as other hidden factors (e.g., the quality of the movie itself) may also play a role. Therefore, reliance on correlation in traditional models might lead to misjudgments and fail to accurately capture the true drivers of box office results.

To better identify and understand these complex relationships, Pearl (2009) proposed causal inference theory, which provides foundational tools for modeling causal relationships in complex systems[6]. The core idea of causal inference is to distinguish correlation from causation and to describe causal relationships between variables using mathematical models.

In Pearl's causal inference theory, Causal Graphical Models (CGM) are important tools for depicting causal relationships. Causal graphs are directed acyclic graphs (DAGs) where nodes represent random variables and edges represent causal influences. Through this graph structure, researchers can identify which variables are drivers of causal relationships and which are confounders or mediators. Causal inference typically involves the following key steps:

Representation of Causal Structure: Using a causal graph model to show the direct and indirect impacts of different movie attributes (e.g., genres, actors, marketing budgets) on box office results.
Estimation of Causal Effects: Quantifying the strength of causal relationships using instrumental variables or counterfactual inference methods.
Handling of Confounding Factors: Using causal inference to control factors that might confound causal relationships during prediction.

A typical application of causal inference is using counterfactual analysis to evaluate whether the box office would have decreased if the marketing budget had not been increased. Such analyses provide decision-makers with stronger explanatory power than correlation analysis.

In movie box office prediction, multiple variables may influence each other. For instance, an actor's fame might directly affect box office revenue, while a movie's marketing budget might be related to both the choice of actors and the increase in audience awareness, indirectly affecting the box office. Therefore, it is necessary to use a causal graph model to depict the complex relationships between these variables and identify the main drivers of box office results.

Specific steps in applying causal graph models in movie box office prediction might include:

Identification of Key Variables: Such as movie genre, director, cast, marketing budget, and release schedule.
Construction of Causal Structure: Connecting these variables with directed edges to show potential causal relationships. For example, the movie genre might affect the size of the target audience, while the fame of the actors might enhance the movie's market appeal.
Inference of Causal Effects: Quantifying the impact of each variable on the box office through the model, avoiding confusion of causal order.

For example, a causal graph might assume that the marketing budget is a dependent variable influenced by movie genre, cast, and release schedule, while the box office is the joint outcome of the marketing budget, release schedule, and cast. Such a causal structure can help understand how different factors collectively affect movie box office revenue and quantify their causal effects.

As deep learning has become widely used in big data, Louizos et al. (2017) further explored the possibility of inferring causal effects in high-dimensional data by combining causal inference with deep learning models[7]. Traditional causal inference methods might face difficulties in handling large-scale and complex data, especially when there are many confounding variables, making the identification of causal relationships unclear. To address this, Louizos et al. proposed using deep latent variable models to identify potential causal structures and infer causal effects in high-dimensional data.

Specifically, deep learning models can automatically extract latent features from complex movie metadata or sentiment analysis results and combine them with a causal inference framework, effectively identifying and estimating causal relationships in high-dimensional, complex data environments. The key advantage of this combined approach is:

Representation Learning of High-Dimensional Data: Extracting higher-order features through deep learning from complex movie metadata or sentiment analysis results, such as historical box office performances of actors or audience rating trends of movies.
Estimation of Causal Effects: Identifying the direct and indirect impacts of these higher-order features on movie box office revenue through the causal inference framework.

This method's strength lies in its ability to identify potential causal relationships in massive movie data and sentiment analysis data, avoiding the traditional issues of relying solely on correlation analysis. Especially in movie box office prediction, deep learning models can better capture nonlinear and complex causal effects.

Compared to traditional correlation analysis, causal inference in movie box office prediction offers the following advantages:

Avoidance of Confounding Effects: Traditional correlation analysis might mistakenly treat some superficially related variables as driving factors, while causal inference can control confounding variables through causal graph models to accurately identify true causal relationships.
Enhanced Predictive Explanability: Causal inference not only provides predictive outcomes but also explains how each variable influences the box office through causal chains, offering decision-makers more transparent and specific recommendations.
Decision Support: Through counterfactual inference, causal inference can help analyze the potential impacts of different decision scenarios on the box office, providing better decision support for movie production and marketing strategies.

Causal inference and causal graphical models offer new perspectives and tools for movie box office prediction. Compared to traditional correlation analysis methods, causal inference not only uncovers deeper causal relationships between variables but also provides decision support based on causal relationships for movie investors.

4. Related Work

In the field of movie box office prediction, scholars have extensively explored how to use different data sources and methods to improve prediction accuracy. Building on this, this paper focuses on reviewing related work in movie box office prediction using causal analysis methods, covering methods based on metadata, text analysis, sentiment analysis, and causal inference. These studies provide a solid foundation for building a Causal Graphical Model (CGM) in this project.

4.1. Movie Box Office Prediction Based on Metadata

Predictions based on movie metadata are one of the most common methods, where researchers use basic information such as directors, actors, film genres, budgets, and schedules to build machine learning models.

Predictions based on movie metadata commonly employ various pre-production features (e.g., directors, actors, genres, budgets, release schedules) to construct predictive models. These data provide valuable insights for box office predictions. Common metadata includes:

Directors and Screenwriters: The influence and fame of directors’ past works may significantly impact box office results.
Cast: The star effect is considered one of the main factors in attracting audiences.
Movie Genre: Different genres, such as action, romance, or science fiction, attract varying audience demographics.
Budget: Both production and marketing budgets can directly influence the quality and market exposure of a movie.
Release Schedule: The choice of release timing (e.g., holidays, summer blockbusters) significantly affects a movie’s box office performance.

These features are typically input into machine learning models as independent variables to predict box office outcomes (often the opening weekend or total gross).

Zhang et al. (2021) utilized these metadata to predict box office performance using multiple regression, decision trees, and neural networks, demonstrating the contributions of different metadata features to movie success[1]. Duan et al. (2008) revealed the impacts of various movie attributes on box office by analyzing panel data from online reviews and metadata[2].

Common machine learning models used include multiple regression, decision trees, random forests, Support Vector Machines (SVM), and neural networks. Here are some commonly used models:

4.1.1 Multiple Linear Regression Model

This model assumes the box office is a linear combination of movie metadata, with the prediction formula:

where is the predicted box office, is the intercept, are regression coefficients, and represent features such as directors, actors, and movie genres. The regression model minimizes error using the least squares method:

where is the actual box office value, and is the predicted value.

4.1.2. Decision Tree Model

Decision trees predict the box office by recursively splitting the dataset into multiple subsets. Each split chooses the feature that maximizes information gain. The information gain formula is:

where is the entropy of the dataset , is the feature used for splitting, are the subsets after splitting, and are the possible values of feature .

4.1.3. Random Forest Model

Random forests are ensemble learning models based on decision trees. They enhance prediction accuracy by averaging (for regression tasks) or voting (for classification tasks) outputs from multiple decision trees. This model is particularly effective in handling high-dimensional data.

4.1.4. Support Vector Machine (SVM)

SVMs create a hyperplane to separate samples in feature space for classification or regression tasks. In box office prediction, the regression form of SVM (SVR) minimizes prediction errors by maximizing the margin, with the objective function:

satisfying:

where is the weight vector, are input features, is the bias, is the actual box office value, and is the tolerated error margin.

4.1.5. Neural Network Model

Neural networks model complex relationships between features through multiple layers of nonlinear transformations. They typically output a predicted box office value. A simple single-layer neural network formula is:

where is an activation function (e.g., ReLU, Sigmoid), is the weight vector, are input features, and is the bias. Neural networks minimize loss functions (e.g., mean squared error) through backpropagation:

4.1.6. Bayesian Regression

Bayesian regression introduces concepts of prior and posterior probabilities in regression analysis. It models regression coefficients with prior knowledge, resulting in a probability distribution of predicted box office values rather than a single prediction. The Bayesian regression formula is:

where is the posterior probability given data , is the likelihood function, and is the prior distribution of regression coefficients.

4.2. Text-Based Sentiment Analysis

The flourishing of social media and online movie reviews has made comment data an important resource for movie box office predictions. Audience comments on social platforms, blogs, and review websites not only reflect their attitudes towards movies but also provide a source of sentiment data for box office predictions.

Duan et al. (2008) explored the relationship between the sentiment polarity of reviews and box office by combining sentiment analysis with comment data[2].

Since then, researchers have explored how to extract valuable information from large amounts of text data through sentiment analysis techniques to predict movie box office performance.

Liu (2012) proposed sentiment analysis technology as a crucial tool in this field[3]. The core of sentiment analysis is to break down comment texts into sentiment polarity (positive/negative) and emotion intensity to identify the audience's attitude towards movies. The main steps in sentiment analysis include:

Text Preprocessing: Removing stopwords, punctuation, and noise data, and tokenizing the text.
Sentiment Lexicon Matching: Mapping words in the text to their corresponding sentiment polarities and intensities using a sentiment lexicon (e.g., SentiWordNet).
Sentiment Classification: Classifying text sentiment using machine learning models (e.g., Naive Bayes, SVM, deep learning models) or rule-based methods.
Sentiment Aggregation: Aggregating sentiment information from individual comments to score the overall movie sentiment, such as calculating the proportion of positive reviews or the average sentiment score.

This method not only quantitatively measures the overall sentiment of the audience towards the movie but also provides a new dimension for predicting box office success—whether the audience's emotional feedback correlates with commercial success.

Mishne and Glance (2006) demonstrated the potential of sentiment analysis in box office prediction through an early study analyzing sentiment data from blogs and review websites[4]. They extracted sentiment polarities from online reviews and compared them with movie box office data, finding a close relationship between sentiment tendencies and first-week box office performance. Specifically, their model used the following core indicators:

Sentiment Tendency Distribution: Analyzing the proportion of positive and negative comments in reviews.
Trend of Comment Sentiment: Observing changes in sentiment during the movie's release period to identify concentrated bursts of negative reviews (e.g., receiving initial praise but a surge in negative reviews later).
Emotion Intensity and Audience Engagement: Quantifying audience engagement by analyzing the word count and tone intensity of comments.

These sentiment analysis indicators provide valuable auxiliary information for box office predictions, especially in understanding the reasons behind box office fluctuations when market performance is below expectations.

Asur and Huberman (2010) further extended the application of sentiment analysis to social media data, particularly platforms like Twitter. They found that the volume of movie-related discussions and sentiment tendencies could significantly predict box office performance[5]. The study used two key social media indicators:

Discussion Volume: Reflecting the movie's exposure and level of attention on social platforms. Higher discussion volumes generally indicate higher audience interest and expectations.
Sentiment Tendency: Classifying the overall sentiment atmosphere towards the movie through sentiment analysis algorithms to determine whether the general sentiment is positive or negative.

Specifically, the study showed that pre-release discussion volume and sentiment tendencies could predict the movie's first-week box office in advance, often more accurately than traditional market research and advertising effectiveness predictions. This model of prediction based on social media sentiment analysis provides strong support for movie marketing.

Sentiment analysis is often combined with other metadata (e.g., actors, genres, budgets) to construct hybrid models that enhance the accuracy of box office predictions. By incorporating sentiment

analysis data as one of the model inputs, researchers can capture immediate audience feedback and combine it with traditional movie features to make more accurate box office predictions. For example, Sharma and Shrivastava (2019) proposed a hybrid machine learning model that significantly improved box office prediction effectiveness by combining movie metadata with sentiment analysis data.

5. Conclusion

The research in the field of movie box office prediction has integrated various data sources such as metadata, online comments, and social media, and employed various machine learning methods. With the development of causal inference and causal graphical models, box office prediction is no longer merely dependent on correlations between variables but can identify the true influencing factors through causal analysis. These studies provide more tools and methods for future movie box office predictions, aiding investors in making better decisions with limited resources.

6. References

Zhang, X., Qin, X., & Wang, Y. (2021). Predicting box office revenue with movie meta data.
Duan, W., Gu, B., & Whinston, A. B. (2008). Do online reviews matter? An empirical investigation of panel data.
Liu, B. (2012). Sentiment analysis and opinion mining.
Mishne, G., & Glance, N. (2006). Predicting movie sales from blogger sentiment.
Asur, S., & Huberman, B. A. (2010). Predicting the future with social media.
Pearl, J. (2009). Causality: Models, reasoning, and inference. Cambridge University Press.
Louizos, C., Shalit, U., Mooij, J. M., Sontag, D., Zemel, R., & Welling, M. (2017). Causal effect inference with deep latent-variable models.
Peters, J., Janzing, D., & Schölkopf, B. (2017). Elements of causal inference: Foundations and learning algorithms.
Abraham, A. L., Guyonnet-Duperat, V., Le Berre, V., Sarry, J., Bornet, O., & Perrier, J. P. (2019). Structural variants in grapevine (Vitis vinifera L.) genotypes highlight different mechanisms of adaptation to environmental conditions. Frontiers in Genetics, 10, 524. https://doi.org/10.3389/fgene.2019.00524