date: 2024-12-24
title: "ML-Density Estimation"
status: UNFINISHED
author:
- AllenYGY
tags:
- NOTE
publish: TrueML-Density Estimation
Nonparametric Density Estimation
For a random vector x, assuming that it obeys an unknown distribution p(x), the probability of falling into a small area R in the space is
Given
Approximation when
When n is very large, we can approximately think that
Assuming
Final approximation for
To accurately estimate
Fixed area size, counting the number falling into different areas, which includes histogram method and kernel method.
the area size so that the number of samples falling into each area is zero is called K-nearest neighbor method.
Histograms as density models
For low dimensional data we can use a histogram as a density model.
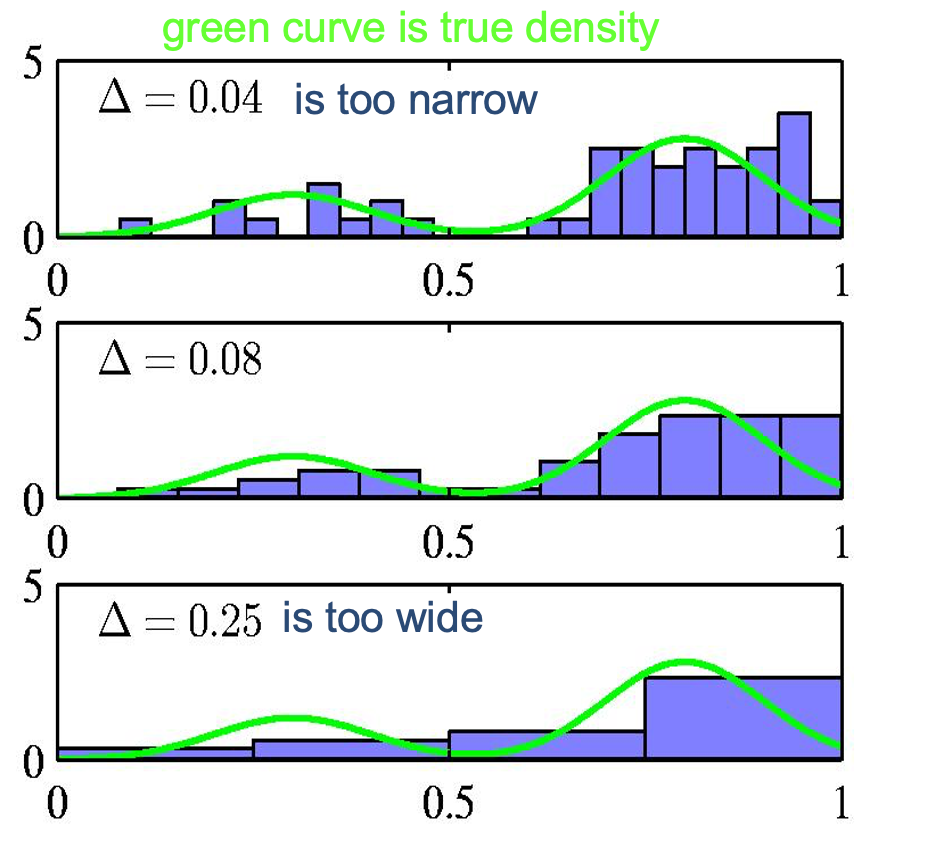
- How wide should the bins be? (width=regulariser)
- Do we want the same bin-width everywhere?
- Do we believe the density is zero for empty bins?
Kernel Density Estimation (KDE)
1. Definition
Kernel Density Estimation (KDE) is a non-parametric method to estimate the probability density function (PDF) of a random variable.
2. KDE Formula
- The kernel function
3. Steps to Compute KDE
- For each data point
- Apply the kernel function to determine the weight of each data point.
- Sum the contributions from all data points and normalize by
4. Example
Data
We have 5 data points:
- Bandwidth
- Gaussian kernel.
Calculation
For each
-
For
-
For
-
For
-
For
-
For
Combine Contributions
The total density at
5. Advantages of KDE
- Flexible: Does not assume a specific distribution of data.
- Smooth: Produces a continuous estimate.
6. Challenges of KDE
- Bandwidth
- Small
- Large
- Small
- Computationally Expensive: Requires evaluating kernel functions for all data points.
Summary
In this example, the estimated density at